그냥 미분 방정식...
예전자료들/잡다한글들
2011. 7. 7. 01:27
위키 백과에서 있던 미분 방정식 예 입니다.
음... 테터툴즈 히스토리 즉, 티스토리에서도 이 수식 기능을 지원 했으면 좋겠습니다.
힘들겠지만...노가다 작업으로 완성할 수 있겠죠. ^^*
음 구성하는건 쉽겠지만, 구현 하는게 조금 힘들려나...;
제차 상미분 방정식
1차 제차 상미분 방정식의 일반형은 다음과 같다.
여기서 f(x)는 우리가 알고 있는 함수이며, 이 방정식은 간단히 변수를 다음과 같이 양변으로 분리하여 놓아서 풀 수 있다.
위 식을 적분하여 다음의 결과를 얻는다.
- y = Ae − F(x)
여기서
A는 임의의 상수이다. (이 결과가 맞는지 확인하려면, 이 식을 원래의 방정식에 대입해 보면 된다.)
f(x)가 상수가 아닌 함수이고, 어떤 함수의 경우에는 (우리가 잘 알고 있더라 하더라도) 그 적분이 불가능 할 수도 있기 때문에, 실제적인 풀이는 매우 어려울 수 있다.
[편집] 1차 비제차 상미분 방정식
1차 선형 상미분 방정식 중 일부는 위의 예처럼 분리가 불가능하다. 이와 같은 1차 비제차 상미분 방정식을 풀기 위해선 적분인자를 알아야 한다. 이 방법을 아래에 설명하고 있다.
1차 상미분 방정식의 일반적인 형태를 생각해 보자.
이 방정식을 푸는 방법은 특별한 "적분 인자", μ 에 달려있다.
일반적인 1차 상미분 방정식의 양변에 μ를 곱하자.
우리가 선택한 특별한 μ의 성질에 의해 위 식은 다음과 같이 간단한 모양으로 변형된다.
미분에 대한 곱의 법칙에 의해 위 식은 다시 다음과 같이 변형된다.
양변은 적분하면,
를 얻고, 마지막으로 y대해 풀고, μ로 양변을 나누면,
를 얻는다. (μ는 x의 함수이므로 더이상 간단히 할 수는 없다.)
'예전자료들 > 잡다한글들' 카테고리의 다른 글
| 배틀하트 다운로드 및 에디터(에딧/치트/핵) (6) | 2011.07.07 |
|---|---|
| 크로이센 에디트(에딧/핵/치트/크랙) (20) | 2011.07.07 |
| 비가 억수로 오네요! (2) | 2011.07.07 |
| 티스토리 초대장 2장 나누어 드립니다. (11) | 2011.07.07 |
| 비가 내리네요! (3) | 2011.07.07 |
| 필명 변경했습니다! (0) | 2011.07.06 |
| 첨성대는 천문대였다! (1) | 2011.06.05 |
| 이런 곳 있을까? (2) | 2011.05.08 |
| 바탕화면 - Fan! (2) | 2011.05.08 |
| 나의 멀티서버 성. (1) | 2011.05.05 |


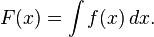
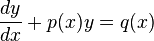
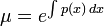
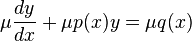

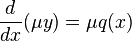


댓글